Koordinat Sistemi

Koordinat sistemi matematikte ve geometride karşımıza çok sık çıkan konulardan biridir. Bu konuyu öğrenmek analitik düşünmeye açılan ilk adımdır. Koordinat sistemiyle denklemleri görselleştirebilir, yer tespiti yapabilir ve matematiksel ifadelerin birbirine göre durumlarını inceleyebiliriz.

Konu çerçevesinde öğreneceğimiz alt başlıklar şöyledir:

Şimdi koordinat sistemi nedir sorusunu yanıtlayarak konuyu öğrenmeye çalışalım.

Düzlemde bir O noktası ve başlangıcı olan birbirine dik e₁ ve e₂ birim vektörleri verilsin. O noktası, e₁ ve e₂ birim vektörlerinin bir arada olduğu sisteme dik koordinat sistemi denir.

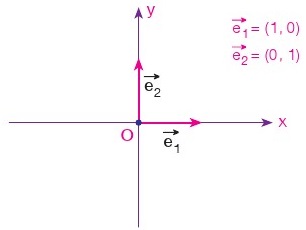
O noktası orjin, e₁ ve e₂ vektörleri birim vektör, bu vektörleri taşıyan doğrulara ise x ve y eksenleri denir.

Dik koordinat sisteminde herhangi bir P(a, b) noktası için merkezden çizilen bir vektör OP = ae₁ + be₂ şeklinde ifade edilebilir.

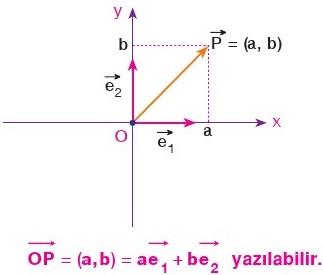
Sonuç olarak bütün vektörleri birbirine dik olan bu iki birim vektörün lineer bileşimi şeklinde yazabiliriz.

Yer Vektörü

Koordinat sisteminde verilen bir vektörün uzunluk, yön ve doğrultusunu değiştirmeden başlangıcını orjine taşırsak elde ettiğimiz şey bu vektörün yer vektörü olur. Yer vektörünün başlangıç noktası orjindir.

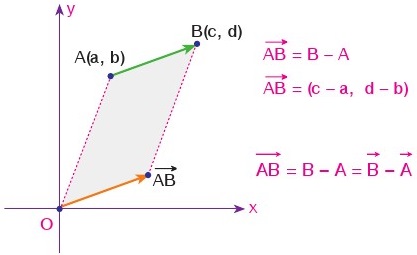
Yukarıdaki şekilde başlangıç noktası A, bitiş noktası B bir vektör verilmiştir. Bu vektörü eğip bükmeden orjine taşıdığımız zaman AB yer vektörü bulunmuş olur. Yer vektörü aynı zamanda konum vektörü olarak da adlandırılır. Örneğin başlangıç noktası A(1, 2) noktası olan ve bitiş noktası B(4, 10) noktası olan vektörün yer vektörü AB = (4 - 1, 10 - 2) = (3, 8) olur. Bu vektörün başlangıç noktasını (0, 0) noktası yaptığımız için sadece bitiş noktasıyla yer vektörünü tanımlamış olduk.

A = (x, y), B = (z, t) vektörleri verilsin.

• A + B = (x + z, y + t) olur.
• A - B = (x - z, y - t) olur.
• k.A = (k.x, k.y) olur.
• A = B = x = z ve y = t olur.

Skaler Çarpım (Öklid İç Çarpımı)

A = (x, y) ve B = (z, t) vektörlerinin skaler çarpımını gösterelim.

<A, B> = x.z + y.t şeklide tanımlanır.

Örnek: K = (-2, 3) ve L = (4, 2) vektörleri için <K, L> iç çarpımını bulunuz.

Çözüm: Yukarıda gösterdiğimiz gibi apsis ve ordinat değerlerini birbiriyle çarpıp toplarız. -2.4 = -8, 3.2 = 6 öyleyse <K, L> = -8 + 6 = 2 olur.

Bazı skaler çarpım soruları geometrik şekil üzerinden verilir. Bu durumda en iyi yöntem, çarpılacak vektörlerin yer vektörlerini bulmak olur. Vektörlerin kuyruğunu orjine taşıyın, başının bulunduğu noktayı kaydedin, sonra da istenilen vektörle gösterdiğimiz gibi çarpın.

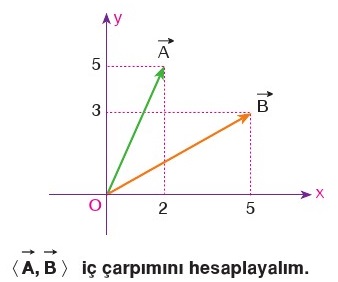
Yukarıdaki soru örneğinde A ve B vektörleri yer vektörü olarak verilmiştir. Bu durumda iç çarpımı bulmak için ihtiyacımız olan şey vektörlerin bal bölgelerinin olduğu noktaları çarpıp toplamaktır. A(2, 5) ile B(5, 3) noktalarını çarparsak 2.5 + 5.3 = 25 olur.

Bazen sorularda vektörler yer vektörü olarak verilmez. Bu durumda AB vektörü için B noktasından A noktasını çıkarmak gerekir.

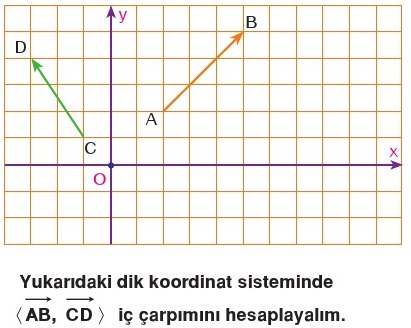
Yukarıdaki örnekte AB vektörünün yer vektörü B(5, 5) - A(2, 2) = (3, 3) olur. (AB vektörü 3 birim sağa 3 birim yukarı kaymış. Şekil üzerinden kaydırdığımızda da bu görünüyor.)

CD vektörünün yer vektörü ise D(-3, 4) - C(-1, 1) = (-2, 3) olur. (Yatayda -2 birim, düşeyde 3 birimlik bir vektör olduğu görülüyor zaten.)

Öyleyse bu iki vektörün iç çarpımı 3.-2 + 3.3 = 3 olur.

<A, B> = k ise <m.A, n.B> = m.n.k olur.

Bir Vektörün Uzunluğu (Normu)

Dik koordinat sisteminde verilen A(a, b) vektörünün uzunluğu ||A|| veya |A| ile gösterilir.

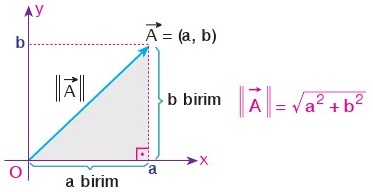
Vektörün uzunluğu Pisagor bağıntısı ile bulunur. |A| = √(a² + b²) olur.

Bu da bir vektörün kendisiyle iç çarpılmasının karekökünün alınması demektir. Yani |A| = √(<A, A>) olur.

Örnek: A(3, 4) vektörünün uzunluğunu bulunuz.

Çözüm: Vektörün uzunluğu 3, 4, 5 üçgeni gereğince 5 olacaktır.

Birim Vektör

Uzunluğu 1 birim olan vektöre birim vektör denir. |A| = 1 bir birim vektördür.

Aşağıdaki vektörlerden hangileri birim vektördür?

• A(1, 0)
• B(0, 1)
• C(-1, 1)
• D(3/5, 4/5)

Uzunluğu 1 birim olanlar birim vektördür. Pisagor bağıntısını kullanarak birim vektör bulmayı öğrendik yukarıda. Buna göre A, B ve D vektörleri birim vektör olur. C vektörü birim vektör olmaz.

D(3, 4) vektörünün uzunluğu 5 birim olduğuna göre (3/5, 4/5) vektörü bir birim vektör olacaktır.

Örneğin, 5 birim uzunluğundaki bir doğru parçasını 5 eşit parçaya bölersek her parçanın uzunluğu 1 birim olur. Bu durum vektörel olarak da düşünülürse her bir parça birim vektöre model olabilir.

Bir Vektörle Aynı Doğrultuda ve Aynı Yöndeki Birim Vektör

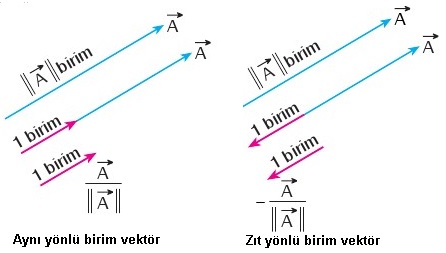
Birim vektör başka bir vektörü belirten doğrultu vektörü olabilir. Bir vektörü uzunluğuna böldüğümüz zaman birim vektörü elde ettiğimizi söylemiştik. Bunu yaptığımızda ortaya çıkan birim vektör esas vektörle aynı yön ve doğrultuda olur.

A vektörü ile A/|A| birim vektörü aynı doğrultu ve yöndedir.

K(8, 15) vektörü olsun. Bu vektörün uzunluğunu hesaplarsak (8 15 17 üçgeni) 17 buluruz. Öyleyse K vektörü ile aynı doğrultuda ve yöndeki birim vektör (8/17, 15/17) olur.

Bir Vektörle Aynı Doğrultuda ve Zıt Yöndeki Birim Vektör

Bir vektörün birim vektörünü bulursak hep aynı yönlü hem aynı doğrultulu olur demiştik. Eğer doğrultuyu değiştirmeden zıt yönlü birim vektör elde etmek istiyorsak - ile çarpmamız gerekir.

A vektörü ile aynı doğrultuda fakat zıt yönlü birim vektör -A/|A| vektörü olur.

İki Vektör Arasındaki Açı

İki vektör bir araya geldiğinde bir açı oluştururlar. Ancak dikkat edilmesi gereken açının doğru taraftan alındığıdır.

İki vektör arasındaki açı vektörlerin kuyrukları aynı nokta olduğunda ortaya çıkar. Birinin başı birinin kuyruğunda değiyorsa o zaman vektörlerden birini taşıyıp kuyruk kuyruğa getirmemiz gerekir.

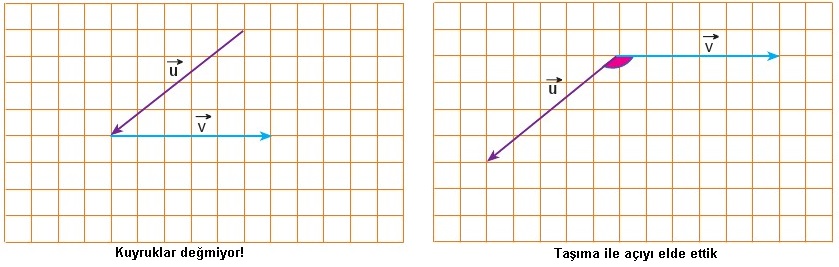
Vektörler arasındaki açıyı iç çarpımda kullanacağız.

Geometrik İç Çarpım

Yukarıda vektörlerin iç çarpımını görmüştük. Burada skaler iç çarpımı geometrik olarak nasıl yapacağımızı öğreneceğiz. Unutmayın ikisinde de sonuç aynı çıkacaktır.

Aralarındaki açı a olan A ve B vektörlerinin iç çarpımı <A, B> = |A|.|B|.cosa olur.

Bazı sorularda iç çarpım yapmak için koordinat sistemine taşımak zor olabilir. Bu durumda aradaki açı bilinirse kosinüs yardımıyla iç çarpım geometrik olarak bulunur.

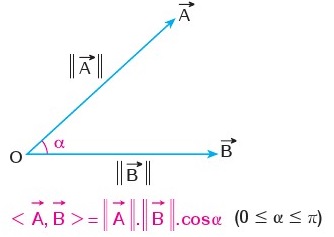
İki vektör arasındaki açının hangi aralıkta olduğuna dikkat etmek gerekir. Örneğin 90 ile 270 derece arasındaki geniş açılarda kosinüs negatif değer almaktadır.

Dik İzdüşüm

Dik izdüşüm gölge mantığının geometriye yansımasıdır. Bir geometrik yapının üzerine yer düzlemine dik bir ışık geldiğinde yerde oluşan gölge o yapının dik izdüşümüdür.

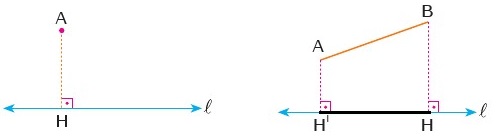
Yukarıdaki şekilde A noktasının ℓ doğrusu üzerine dik izdüşümü H noktasıdır. Yine aynı şekilde [AB] doğru parçasının dik izdüşümü ise [H'H] doğru parçasıdır.

Bir Vektörün Bir Doğru Üzerindeki Dik İzdüşüm Vektörü

Başlangıç noktaları aynı olan A ve B vektörleri verilsin. A vektörünün B vektörü üzerindeki izdüşümü OH vektörü olsun.

OH vektörünün uzunluğu bulunurken A ve B vektörlerinin iç çarpımı B vektörünün uzunluğuna bölünür.

OH vektörünün uzunluğu bulunduktan sonra bu vektör B vektörü üzerinde olacağı için B vektörünün doğrultu birim vektörüyle çarpılır. Uzunluk ile birim vektör çarpılınca OH vektörünün kendisi ortaya çıkar.

Burada dikkat edilmesi gereken OH vektörü ile |OH| uzunluğunun karıştırılmamasıdır.

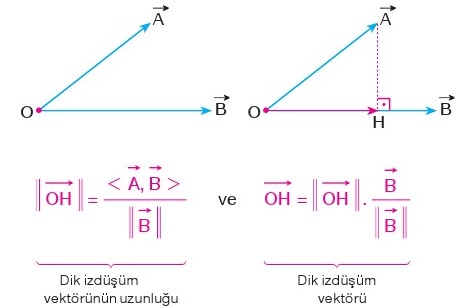
Yani önce izdüşüm vektörünün uzunluğu bulunur. Sonra doğrultu birim vektörüyle çarpılıp vektör elde edilir. Yukarıdaki resimde formüller verilmiştir.